The Wise son:
In the previous post, we discussed non-inferiority (NI) study design. The first thing you need for establishing sample size for NI study, is to establish the NI-Margin (margin). It may be necessary to evaluate the sample-size (N) sensitivity to a range of margins. Small margin may require unrealistic large sample size, while larger margin may not be clinically accepted as a non-inferiority.
The Simple son:
The sample size for a non-inferiority trial with a custom power of 85% is calculated to satisfy the following Chow, 2017 equation:
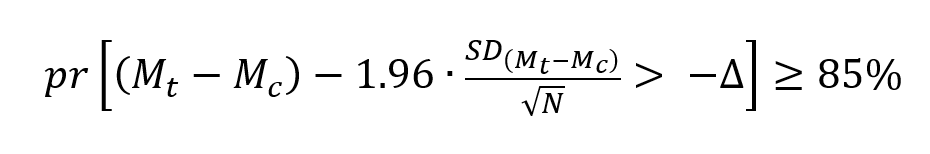
Where:

In words, the sample size must be large enough so that the probability is sufficiently high that the lower bound of the 95% CI for the estimated means difference between the treatment and the control (or reference) products, (Mt-Mc) is greater than the NI margin (Δ).
The Wicked son:
Let’s see who understands formulas, shall we? OK then,
Which of the following cases requires the largest N?
- Large margin (Δ), large standard deviation (SD).
- Large margin (Δ), small standard deviation (SD).
- Small margin (Δ), large standard deviation (SD).
The Simple son:
Wicked, you’re not scaring anyone. We can use R to perform a simulation to test that, for a trial with 2 equal-sized groups:
library(SampleSize4ClinicalTrials)
margins <- c(-0.5, -0.75, -1, -1.5, -2, -2.5)
powers <- c(0.8, 0.85, 0.9, 0.95)
SDs <- c(3.7, 3, 2.5, 2)
tab1 <- data.frame(Margin = c(), SD = c(), N = c())
list_tab <- list()
for (P in 1:length(powers)) {
for (j in 1:length(SDs)) {
for (i in 1:length(margins)) {
N <- as.numeric(ssc_meancomp(design = 3L, ratio = 1, alpha = 0.05, power = powers[P], sd = SDs[j], theta = 0, delta = margins[i])[1])
tab1 <- rbind(tab1,
data.frame(Margin = c(margins[i]), SD = c(SDs[j]), N = N) )
}
}
list_tab[[P]] <- tab1
tab1 <- data.frame(Margin = c(), SD = c(), N = c())
}
tab_final <- cbind(list_tab[[1]], list_tab[[2]][,3], list_tab[[3]][,3], list_tab[[4]][,3])
names(tab_final) <- c("Margin", "SD", "N.80%", "N.85%","N.90%","N.95%")
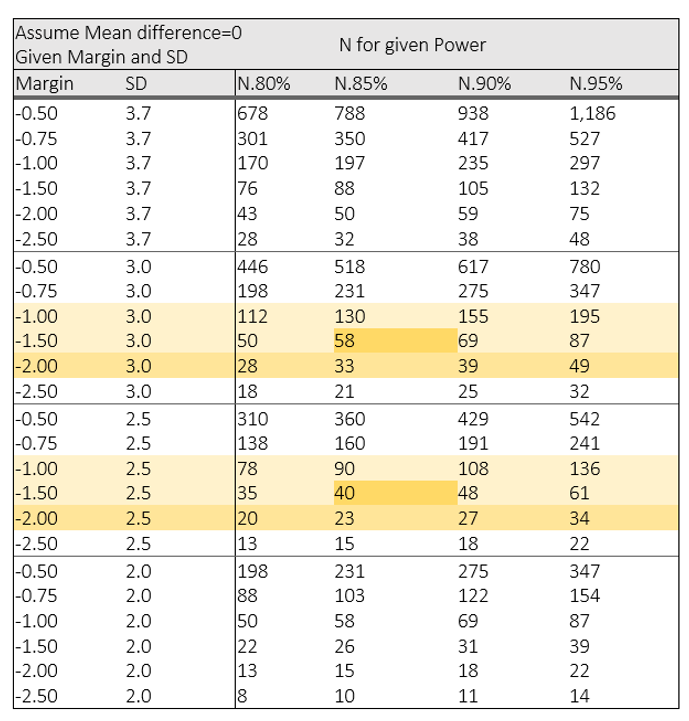
So, the answer to your question, Wicked, is the third case; small margin and big standard deviation yields the largest sample size.
He who couldn’t ask:
It took me a few hours to understand that “SampleSize4ClinicalTrials” means “sample size for clinical trials”. Nobody teaches you those things, they all just expect you to understand everything.

